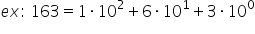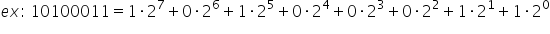Sistemul de numerație zecimal și sistemul de numerație binar

să vorbim acum despre sistemul

de numerație zecimal și sistemul

de numerație binar pare un titlu

complicat însă să știți o lecție

destul de interesantă și acum ca

să ajungem la sistemul de numerație

zecimal Haideți să ne gândim puțin

la cifrele pe care le folosim noi

pe noi folosim cifre de la 0 până

la 9:00 însă să știți că lucrurile

nu au fost așa de la începutul

apariției sau evoluției oamenilor

oamenii preistorici Probabil că

foloseau în alt sistem de numerație

de exemplu ca să ajungă de la un

loc la altul și să vadă cum Care

este numărul zilelor petrecute

pe drum gândeam în felul următor

Deci mergea o zi mergeau încă una

mergeau Încă una și încă una așa

cât de cât își făceau o idee despre

durata drumului respectiv Însă

este clar că odată ce avem din

ce în ce mai multe asemenea liniuțe

adică folosim acest simbol de mult

mai multe ori e mult mai ușor să

Ne încurcăm în această numărătoare

de aceea Era clar că omenirea avea

nevoie de un sistem de numerație

mult mai simplu mesopotamienii

avea un alt sistem de numerație

Iată acest triunghi însemnat numărul

1 acesta numărul 10 iar acesta

numărul 60 dacă am fi vrut să scriem

de exemplu numărul 23 Iată foloseam

două asemenea triunghiuri care

reprezintă împreună numărul 28

încă trei echipe tenii foloseau

alte simboluri Iată avem aici numărul

unu o liniuță numărul cinci rare

prezentat de cinci liniuțe acest

arc reprezenta numărul 10 pergamentul

îndoit reprezenta numărul 100 floarea

de lotus adică acest simbol numărul

1.000 și degetul arătător 10.000

însă Toate aceste sisteme de numerație

ce am prezentat până acum sunt

destul de complicate și de aceea

sa dorit construirea unui sistem

de numerație mult mai simplu Se

presupune că datorită faptului

că oamenii au 10 degete atunci

sau construit un sistem de numerație

zecimal adică un sistem de numerație

în baza 10 cele 10 simboluri ale

acestui sistem de numerație zecimal

sunt cifrele 0 1 2 3 4 5 6 7 8

și 9 ele reprezintă ele sunt de

fapt doar niște simboluri cu ajutorul

cărora a fost construit acest sistem

de numerație zecimal să știți că

există și alte sisteme de numerație

avem de exemplu sistemul de numerație

în baza 2 Stăm aici baza 2 acesta

se mai numește și și sistem de

numerație binar acum dacă la sistemul

de numerație în baza 10 am avut

10 simboluri la acesta în baza

doi câte simboluri vom avea păi

doar două Care sunt acelea aici

am avut toate numerele naturale

de la zero și au fost stick mai

mici ca zece aici tot așa avem

toate numerele naturale de la zero

strig mai mici ca doi adică 0:01

Cum scriem acum un număr în baza

10 Păi Haideți să luăm Ca exemplu

numărul 163 Păi îl putem scrie

în felul următor trece în prima

cifră urmată doar de zerouri adică

avem numărul 100 adunate cu 63

procedăm la fel pentru 63 decise

să scriu pe 100 avem șase urmat

dor des zerouri avem nevoie de

fac doar de un singur 0 plus 3

și acum noi vrem să evidențiem

această bază 10 să vedem cum facem

acest lucru Păi pe 100 îl putem

scrie 10 la a doua sau 1 înmulțit

cu 10 la a doua o să înțelegeți

imediat De ce am pus unul înmulțit

cu plus aici avem 60 adică 6 înmulțit

cu 10 adică 10 la întâia adunat

cu 3 Păi pe 3 poți să îl scriu

3 ori 1 însă pe 1 pot să scriu

ca o putere cu baza 10 și anume

10 la exponentul 0 Păi iată că

astfel prin aceste puteri ale lui

10 a evidențiat că am aici un număr

care este scris în baza zece pentru

baza doi ce vom avea Păi nu vom

avea puteri ale lui 10 și vom avea

puteri ale lui doi și vom vedea

Facebook cu imediat însă înainte

Haide să ne mai uităm puțin la

numărul 163 era normal că acest

număr să fie scris astfel pentru

că ea atât 3 este cifra unităților

dar avem aici trei ori 1 aici avem

cifra zecilor și noi avem șase

zeci adică 6 ori 10 iar aceasta

este cifra sutelor adică avem 1

înmulțit cu 100 de aceea am scris

aici 1% ca să evidențiem clar cifrele

care apar 1 6 și 3 Dacă facem suma

iar obținem exact ce avem aici

adică numărul 163 Deci am putea

să scriem astfel Aici este locul

unităților adică 10:00 la 0 care

înseamnă 1 aici avem locul zecilor

adică 10 la puterea întâia iar

Aici avem locul sutelor 110 Pardon

la puterea a doua cum am spus dacă

în sistemul de numerație zecimal

avem puteri ale lui 10 în sistemul

de numerație binar avem puteri

ale lui doi și anume vom avea Haide

să luptăm așa Să presupunem că

acest avem aici un număr cu mai

multe cifre scrise în baza 2 și

vom avea doi la zero Haide să scriem

de aici 2 la 0 aici este locul

unităților aici nu vom mai avea

locul zecilor ca aici și putem

să spunem că avem locul doi lor

că avem practic 2 la n tăia aici

vom avea doi la două doi la a treia

Deci același lucru însă în loc

de bază 10 avem baza 2 2 la a patra

2 la a cincea 2 la a 6-a și 2 la

a șaptea bun să știți că acest

număr 163 scris în baza doi este

acesta și avem unu zero urmat de

unu apoi zero zero zero unu și

unu e bine acest număr pe care

îl vedeți aici este un număr scris

în baza 2 Un număr scris doar cu

aceste simboluri 0:01 sistemul

de numerație binar Este cel care

stă la baza calculatoarelor de

ce Pentru că bitul adică acea celulă

să îi spunem așa de bază poate

lua valoarea 1 sau zero Adică poate

să treacă sau să nu treacă curent

prin celula respectivă și orice

operație făcută de calculator este

făcută în sistem binar de exemplu

dacă noi vrem să calculăm această

sumă a 13 plus să nouă calculatorul

lucrează în spate să spunem așa

doar cu aceste numere Deci transformă

numerele din baza 10 în baza 2

și apoi lucrează cu ele în baza

2 acum pe lângă această Lăsând

la o parte această curiozitate

Haideți să vedem Cum ajungem de

la un număr scris în baza doi de

exemplu acesta la un număr scris

în baza 10 e clar că Transformând

acest număr din baza 2 în baza

10 trebuie să obținem numărul 163

bun Cum facem asta pe aici avem

locul unităților și observăm că

avem cifra 1 Deci avem practic

1 înmulțit cu evidențiem faptul

că unul e unitate Prin înmulțirea

cu 2 la 0 acum aici nu avem în

locul zecilor și locul 2 lor dacă

vorbim de bază 2 și avem simbolul

1 înmulțit cu 2 la întâia apoi

avem 0 înmulțit cu 2 la a doua

apoi avem 0 din nou înmulțit acum

cu 2 la a treia dar apoi Tot zero

înmulțit cu 2 la a patra apoi 1

înmulțit cu 2 la a cincea 0 îl

înmulțim cu 2 la a șasea și pe

1 în final îl înmulțim cu 2 la

a șaptea prin însumarea acestor

numere care atenție Acum sunt numere

scrise în baza 10 trebuie să obținem

numărul 163 vom avea așa o 2 la

a șaptea înseamnă 128 1 128 ne

dă 128 aici obținem 0 aici vom

avea doi la cincea 32 ori unu Deci

32 aici Tot zero zero zero 0 1

Mai 1 ori 2 la 1 an de 2 2 la 0

înseamnă 1 înmulțit cu 1 ne dă

1 și idee să trecem și operația

de adunare între aceste numere

cât obținem Păi avem 128 cu 32

cu 2 cu 1 Deci cu 3 Rezultatul

este 163 Haideți să mutăm aici

163 de ceartă că am obținut între

adevărat chest număr acum în exerciții

putem să notăm astfel de ce avem

acest număr 1:01 mei de trei de

0 și 2 de 1 în baza 2 ca să evidențiem

că vorbim de bază 2 aici în paranteză

trecem numărul 2 și arătăm că avem

un număr scris în baza 2 Cum îl

transformăm în baza 10 Păi exact

ca aici însă putem să începem cu

ultima cifră și vom avea așa unul

multe cu și avem puterea 0 a lui

2 adică 2 la 0 plus 1 acest 1 înmulțit

cu 2 la 1 a plus 0 ori următoarea

puterea lui 2 adică 2 la a doua

cu alte cuvinte obținem exact această

sumă însă termenii sunt scriși

invers de la dreapta la stânga

plus De ce am făcut acest zero

rimează încă un zero înmulțit cu

2 la a treia plus încă un zero

adică acesta înmulțit cu 2 la a

patra plus urmează aici un 1 ori

2 la a cincea plus 0 ori 2 la a

șasea și în final mai avem 1 ori

2 la a șaptea Păi avem exact aceeași

sumă ca aici și am obținut numărul

163 pe care îl putem Scrie în baza

10 astfel putem să notăm aici numărul

10 Și asta înseamnă că avem un

număr în baza 10 Nu e neapărat

nevoie să scriem baza atunci când

avem baza zece pentru că e baza

pe care o folosim cel mai des Haideți

să mai facem încă un exemplu și

să transformăm din baza 2 în baza

10 acest număr 1 0 0 1 0 Deci avem

baza 2 cum notăm Păi avem prima

cifră de aici 0 înmulțit cu puterea

0 a lui 2 adică 2 la 0 adunat cu

urmează apoi 1 înmulțit cu 2 la

întâia adunat cu zero ori 2 la

a doua adunat cu zero acest zero

înmulțit cu 2 la a treia adunat

cu unu în munți cu 2 la a patra

și vom avea așa 0 aici avem Doina

unui ani de 2 ori 1 2 plus aici

ne dă 0 plus din nou 0 doina 4-a

este 16 înmulțit cu 1 Deci 16 care

rezultatul Păi avem 16 adunat cu

2 deci ne dă 18 Deci ca să transformăm

un număr din baza 2 în baza 10

Haideți să scriu aici vom face

această sumă și vom lua pe rând

puterile lui 2